I found this really interesting paper that explains on Nagajruna's logic, but in modern day terms. It is interesting that Nagajurna conveyed the Dharma in a method that is only discovered 1.5k years later. Also this logic was used by the Buddha to describe emptiness as well. Have a read, although it is...quite difficult to understand, still.
Abstract. Numerous authors over the centuries have puzzled over what has been called “the Buddhist paradigm of catu?ko?i.” A classic example: the four statements, considered both mutually exclusive and jointly exhaustive,
(i) the Tath?gata exists after death;
(ii) the Tath?gata does not exist after death;
(iii) the Tath?gata both does and does not exist after death;
(iv) the Tath?gata neither does nor does not exist after death.
We offer some linguistic gedanken-experiments illustrating everyday situations in which appropriate analogues to these four statement-forms are entirely plausible as mutually exclusive, or jointly exhaustive, alternatives; and we offer a framework, based on the logical paradigms of locale or topos theory, illustrating how forms (iii) and (iv), in particular, need be neither contradictory, nor paradoxical, nor even mutually equivalent.
Foreword
As an exemplary model — what in German might be called a Vorbild or Musterexemplar — of catu?ko?i or tetralemma, one would be hard-pressed to find a more quintessentially perfect instance than the following, taken from verse XVIII.8 of the M?lam?dhyamakak?rik? by N?g?rjuna, as kindly rendered into English by the generous referee:
Anything is either true,
Or not true,
Or both true and not true,
Or neither ... .
This fragment provides what a mathematician of a certain bent might call a universal example of catu?ko?i in all regards — form and content, structure and message — without a single superfluous word or restriction.
Of course, to the reader steeped in the bivalent logical tradition prevalent in the West from the time of Aristotle, or even before, through the time of Boole, and beyond, already the first two lines of this fragment would seem to cover all the bases, with the last two being quite superfluous, little more than incomprehensible, contradictory, mystifying mumbo-jumbo, if not downright misleading mystical nonsense.
The very modest aim of the presentation that follows will be to tease out of the catu?ko?i any lingering fiber of paradox, conundrum, or mysticality, so as to allow such a reader to recognize, in each of the four alternatives that the catu?ko?i sets forth, a familiar, viable, and relevant state of affairs. The means by which to accomplish this aim will number but two: suitable models of (nonstandard) logical systems (cf. [R] for a thorough if technical introduction to such ideas), and examples from everyday language.
The reader expecting anything more will, alas, come away disappointed. Neither the history of the catu?ko?i, nor the role of catu?ko?i in Indian philosophy, nor any critical analysis of their many commentators, nor any sensitive comparisons or contrasts of those commentators, or their comments, one with another — no such scholarly discourse — will be found here. For such material, the reader is better advised to visit the pages of , [C], [G], or [Si], or, even better, the many works cited therein.
Nor will the reader find any attempt to provide information as to the nature of Truth, or Reality, or what it means to be Valid, or to Exist — here again, for etymological as well as for epistemological enlightenment, our advice would be to consult articles like [K] and [Sö], or to browse through the pages of [JIPR] and of its subsequent sister volumes, where similar articles have appeared.
Finally, beyond offering all due gratitude to the reader who can forgive these omissions (and abject apologies to the reader who can not), I must express profound thanks to Professors Emch and Sridharan for having encouraged the preparation of the present material in the first place; to the referee (alas, anonymous), whose numerous valuable suggestions upon an earlier draft I hope I have adequately incorporated into the present revision; to the airlines UAL and Lufthansa, whose frequent flyer program and aircraft, respectively, graciously facilitated my participation in the Bangalore conference by providing complimentary air transport between the North American continent and India; and to the Faculty Research Grant program of Wesleyan University, for its generosity in underwriting selected additional travel expenses connected with the presentation of this material at Bangalore.
Taming the Terrible Catu?ko?i
What the extract from N?g?rjuna cited in the foreword suggests, as regards the catu?ko?i quoted in the abstract (to be found as item /1/ on page 28 of ), is that, writing P for the proposition that “the Tath?gata exists after death,” the four propositions
(i') P
(ii') ¬P (not-P)
(iii') P & ¬P (P and not-P)
(iv') ¬P & ¬¬P (neither P nor not-P)
(corresponding to (i)-(iv)) are mutually exclusive and cover all possibilities. What sort of logic can be at work here?
Classically, of course, at least in the western tradition, where P and ¬P are complementary and ¬¬P = P , the last two formulations are identically trivial and the first two already cover all possibilities (principle of excluded middle, or tertium non datur).
In the intuitionistic logic of a topos, on the other hand — and, unlike in an earlier lecture [L], we shall refrain here from attempting to offer any introduction to the notion of topos, or to the sort of logic prevailing there, preferring to send the interested reader to such standard expositions of those matters as [J] (especially Chapter 5, sections 1 and 2), or [L&S] (especially the marvelously informal overview of pp. 123-128), or [M&M] — the first two formulations are no longer complementary. They do remain mutually exclusive, however, and the last two, consequently, are still identically trivial. It is just that the first two need no longer cover all possibilities, that is, the principle of excluded middle need no longer hold. (Concrete illustrations of such a state of affairs will appear below.)
If, instead, we envision a logic dual to that of a topos, more like the logic of the lattice of closed subsets of a topological space, we finally reach a situation where both P & ¬P and ¬P & ¬¬P may be non-trivial. But now P , ¬P , P & ¬P , and ¬P & ¬¬P may well no longer be mutually exclusive. Indeed, at least for closed P , we have the order-inclusions
¬P & ¬¬P < P & ¬P < P
and
¬P & ¬¬P < P & ¬P < ¬P ,
so that if P is “regular-closed,” say, that is, if P = ¬¬P , the last two formulations coincide and fall within both P and ¬P (indeed, they constitute the boundary of P ).
Somehow, ¬P must not be getting treated purely as the negation of P . Let us write Q temporarily for this negation of P , and see what we can make of statements (i) through (iv) in such a setting. They become
(i") P ,
(ii") Q ,
(iii") P & Q , and
(iv") ¬P & ¬Q ( = ¬(P Ú Q)) ,
where the last formulation is logically tantamount to the negation of “P or Q (or both),” i.e., to the negation of what the first two alone jointly cover. Certainly the last item here excludes each of the earlier ones, and all are, in general, non-trivial. But if all four are to be mutually exclusive, what (i") and (ii") are implicitly intending to represent must surely be rather
(i''') P & ¬Q
and
(ii''') ¬P & Q ,
respectively. Then, at least classically, we obtain the four mutually exclusive, jointly exhaustive, atomic generators of the free Boolean algebra on the two free generators P and Q , viz.:
(a) P & ¬Q = P ? Q ,
(b) ¬P & Q = Q ? P ,
(c) P & Q = P & Q , and
(d) ¬P & ¬Q ( = ¬((P ? Q) Ú (Q ? P) Ú (P & Q)) = ¬(P Ú Q)) .
But how is one now to make any sense of the hope that Q may stand for ¬P ? That is, how shall we maintain the mutual exclusivity and individual non-triviality of the four items
(a') P & ¬¬P ,
(b') ¬P & ¬P ,
(c') P & ¬P , and
(d') ¬P & ¬¬P ,
obtained from (a)-(d) by putting ¬P in place of Q ?
Let us simplify, for the moment, by assuming that ¬¬P = P , so that the four conjunctions above become
(a") P & P ,
(b") ¬P & ¬P ,
(c") P & ¬P , and
(d") ¬P & P .
Next, let us imagine that the second occurence of P in each of these four conjunctions is merely a homonym for the P that occurs first. Mostly, in living languages, homonyms are words that sound alike, but are spelled differently and have different meanings, like red, the color, and read, the past participle, or pear, the fruit, pair, the duo or couple, and pare, the verb meaning to peel (and perhaps also cut up) a fruit (perhaps even a pear) or vegetable. But there are homonyms also with both sound and spelling identical, like sucker, which can at once signify a person easily duped or taken advantage of, or a tendril on a vine.
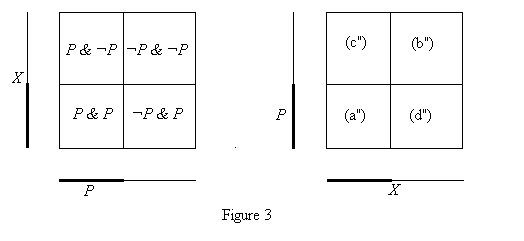
How may we realize the two occurrences of P in (a")-(d") as mere homonyms of each other? It would be enough, for example, were our lattice of propositions somehow spatial, that is, representable as some sort of subsets of some particular space X , to place ourselves in the Cartesian product X ´ X of the space X with itself. For now, corresponding to P , there arise two clearly distinguishable homonyms of P in X ´ X : one, the “vertical cylinder” P ´ X over the P in the first spatial factor X ; the other, the “horizontal cylinder” X ´ P alongside the P in the second factor X (cf. Figures 1 & 2).

If we now simply treat each first occurrence of P in the forms (a")-(d") as instances of the vertical cylinder P ´ X , and each second occurrence as the horizontal one X ´ P , then our four conjunctions correspond to the four rectangles in Figure 3 ( P & P being interpreted, for example, as the intersection, P ´ P, of P ´ X with X ´ P , etc.).
For what it’s worth, we exhibit a topos whose internal logic has system of truth values inherently of this form. Indeed, where S is any of the very classical topoi of absolutely standard sets — say, made up of the sets in Gödel’s constructive hierarchy — the topos S ´ S of ordered pairs of such sets is such a topos. Its truth value object is the ordered pair ( 2, 2 ) consisting of two copies of the usual two-element Boolean algebra formed from the ordinal number 2 = {0, 1}, and this has exactly four global elements: (1, 1) and (0, 0), playing the roles of True and NotTrue , and serving as counterparts of P & P and ¬P & ¬P , respectively; and (1, 0) and (0, 1) , playing the roles of BothTrueAndNotTrue and NeitherTrueNorNotTrue , counterparts in turn of P & ¬P and ¬P & P .
Not every topos whose truth value object has exactly four global elements has them arranged quite in this way, however. For example, if we topologize the ordinal number 3 (whose points are the smaller ordinals 0 , 1 , and 2 ) by declaring open exactly those subsets of 3 that happen themselves to be ordinal numbers (viz., Ø (the empty subset), {0}, {0, 1}, and all of 3 ) , then the topos of sheaves on this space 3 has truth value object whose global elements likewise number four, but correspond exactly, even as to their ordering, to the four open subsets of 3 that make up the topology just described. Here, between True and NotTrue (or 3 and the empty set) we have two intermediate truth values, each neither True nor NotTrue , but one “more true,” as it were, and “less not true,” than the other:
NotTrue = Ø < {0} < {0, 1} < 3 = True .
To within isomorphism, this topos may also be depicted as the topos of double-transitions among sets, that is, as configurations of the form
A ¾¾f® B ¾¾g® C
made up of three sets and two functions, as depicted. The truth value object for this topos is the configuration

where 4 , 3 , and 2 are the ordinal numbers 4 = {0, 1, 2, 3}, 3 = {0, 1, 2}, and 2 = {0, 1}, and the functions f+ and f- both carry 0 to 0 and 1 to 1 , but f-(2) = 1 , while f+(2) = f+(3) = 2 , as depicted above.
The four global elements here are simply the four length-two paths, or orbits, seen to emanate from the various members of 4 , the uppermost and lowermost of which it seems plausible to accept as playing the roles of True and NotTrue , respectively, while the remaining two paths, clearly neither True nor NotTrue , somehow represent the values “more True than NotTrue” and “more NotTrue than True.” Or perhaps the catu?ko?ian expressions “both true and yet not true” and “neither true nor yet not true” better convey the sense of these intermediate truth values, though we suspect this is not an illustration of the classical paradigm the catu?ko?i had in mind.
But in fact, the logic of this topos does realize the way apparent contradictions are commonly used in everyday speech. A daiquiri made with far too much lime juice, for example, and a little too much sugar, may well be called both sweet and not sweet; a coffee prepared with just barely not enough sugar for the taste of a particular coffee-drinker may be disparaged as neither sweet nor not sweet. If the best student to pass through your department in the past ten years has an uncanny knack for getting arrested at student political demonstrations, you will be apt to wonder whether your department should once again post bail for this student who is both really very bright and yet not really very bright. Or, of another student, not quite so bright — generally dealing very well with the more difficult problems and readings, but sometimes inexplicably failing utterly when faced with far simpler ones — and yet having an investment acumen that is simply uncanny, you may well think, somewhat perplexedly, this student is neither really all that bright, nor not really all that bright.
There are, of course, also everyday linguistic settings in which the last two catu?ko?i options (iii) and (iv), far from being mutually exclusive, coincide competely. This state of affairs corresponds, perhaps, to the Trair?sika viewpoint (cf. , p. 35). A grape-fruit, for example, sour, to some extent, like all its kin, but remarkably less so than most, you might be equally happy to describe as both sour and not sour, or as neither sour nor not sour. Would you like a topos whose truth value object epitomizes just this situation, not envisioned in the catu?ko?i, of the last two options (iii) and (iv) coinciding? The Sierpi?ski topos, as it’s known, is a case in point.
The objects of the Sierpi?ski topos are shortened versions of the configurations shown above: only two sets, B and C , rather than three, and only one function g . The truth value object is the right-hand fragment of the truth value object shown above, and has only three global elements, namely the three one-step paths emanating from the various elements of 3 , which have reason to be thought of as True , NeitherWhollyTrueNorNotWhollyTrue , and NotTrue (taken from top to bottom), respectively, though the middle value may equally well be thought of as TrueInTheLongRunEvenIfNotTrueAtTheOutset . This middle truth value, in other words, is at once BothTrueAndNotTrue and NeitherTrueNorNotTrue , and is the only alternative to the extreme values True and NotTrue .
Afterword
As a final topic, perhaps not worthy of even this passing mention, let us take up one objection on the part of some commentators to the tetralemma paradigm, namely, that there should by rights be yet a fifth alternative, something like NoneOfTheAbove , to the classical four. The Buddha himself, after all, is reported in one instance to have rejected, each in its turn, all four alternatives of one particular quadrilemma, indicating that the truth lay somehow elsewhere.
There are indeed topoi, readily described, whose global truth values easily realize the ideal of being five in number. For that matter, that ideal can be realized in three wholly different ways. In all cases, however, the lattice of global truth values must, for purely topos-theoretic reasons (that is, by virtue of what has been called generalized abstract nonsense), be what is known, to those in the lattice trade, as distributive. That requirement rules out the last two lattices depicted in the following Figure 4. The remaining five-element lattices number three: they too appear in Figure 4, as the first three on the left: they are all distributive, but none is Boolean.

Figure 4
And just which of their intermediate members (between True at the top and NotTrue at the bottom) should be interpreted as BothTrueAndNotTrue , as NeitherTrueNorNotTrue , or as NoneOfTheAbove , I leave as my parting conundrum to you.
http://tlvp.net/~fej.math.wes/SIPR_AMS-IndiaDoc-MSIE.htm